Nu skall vi titta på den mer formella definitionen av derivatan.
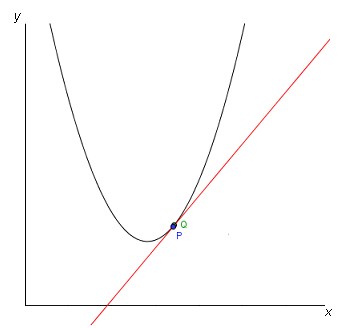
Som vi nämnt tidigare så är derivatan i en viss punkt lika med tangenten till kurvan i denna punkt. Låt oss anta att vi har två punkter, \( P\) (blå) och \( Q\) (grön) längs en kurva så som bilden nedan visar. Genom dessa drar vi en linje.
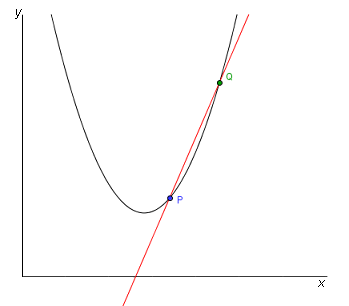
Vi vill veta tangenten till kurvan i punkten \( P\) är. Om vi nu låter \( Q\) närma sig \( P\) får vi ett närmare och närmare värde på tangenten till kurvan i punkten \( P\)! Se bild ovan och bilderna nedan.
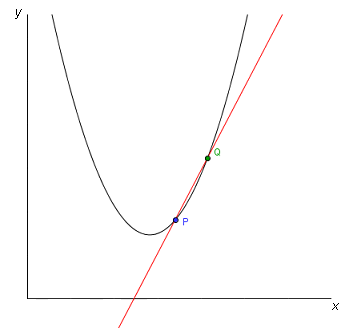
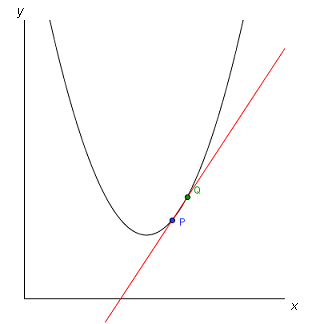
Låt oss använda oss av matematik för att få fram en mer precis definition och den sanna tangenten till kurvan i punkten \( P\)!
Punkten \( P\) har koordinaterna \( (x,f(x))\), och punkten \( Q\) har koordinaterna \( (x + h, f(x+h))\). \( h\) är avståndet mellan punkternas x-koordinater. Bilden nedan illustrerar punkternas läge.
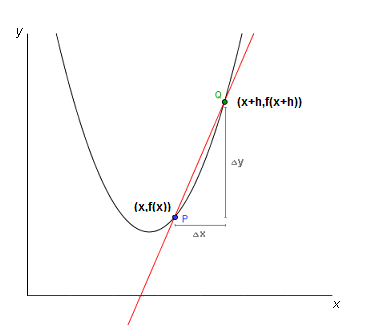
Lutningen för en rät linje är avståndet mellan y-koordinaterna dividerad med avståndet mellan x-koordinaterna. Vilket betyder att vi lätt kan finna lutningen för linjen genom \( P\) och \( Q\).
\(k = \dfrac{\Delta y}{\Delta x} = \dfrac{f(x+h)-f(x)}{x+h-x} = \dfrac{f(x+h)-f(x)}{h}\)
När vi minskar på \( h\) så rör sig \( Q\) allt närmare \( P\). Om vi låter \(h\) gå oändligt nära noll så får vi lutningen för tangenten i punkten \( P\)! Att vi låter \( h\) gå oändligt nära 0 betecknas med \( \lim_{h \to 0}\). Detta leder till derivatans definition
\( \boxed{f'(x)=\lim_{h \to 0}\dfrac{f(x+h)-f(x)}{h}}\)
Derivatan betecknas som \( f'(x)\) och uttalas ”f-prim av x”. Derivatan har olika notationer. De vanligaste är \( f'(x),\ D(f(x)),\ \dfrac{dy}{dx},\ \dfrac{df(x)}{x},\ y’\). Kvoten \( \dfrac{f(x+h)-f(x)}{h}\) kallas för differenskvot.
Nu skall vi börja titta på hur vi kan använda definitionen för att derivera funktioner. I nästa artikel om derivata så kommer vi att titta på enkla regler för derivering som gör att man slipper använda derivatans definition varje gång. Men det är nyttigt att först ha tittat på dess definition samt ha använt den.
Exempel
Derivera följande funktioner med hjälp av derivatans definition \( f'(x)=\lim_{h \to 0}\dfrac{f(x+h)-f(x)}{h}\)
a. \( f(x) = x^2+1\)
b. \( f(x) = 4x + 3\)
c. \( f(x) = x^3\)
Lösningar
a. Det första vi vill göra är att ta reda på \( f(x+h)\) så vi kan stoppa in samtliga värden i derivatans definition.
\( f(x) = x^2+1 \\ f(x+h) = (x+h)^2+1\)
som alltså ger differenskvoten
\( \dfrac{f(x+h)-f(x)}{h} = \dfrac{((x+h)^2+1)-(x^2+1)}{h}\)
men om vi låter \( h\to 0\) (\( h\) gå mot 0) så kommer uttrycket att gå mot \( \dfrac{0}{0}\). Så vi får förenkla differenskvoten innan vi låter \( h\to 0\)
\( \dfrac{(x^2+2xh+h^2+1)-(x^2+1)}{h} = \dfrac{x^2+2xh+h^2+1-x^2-1}{h} = \\ = \dfrac{2xh+h^2}{h} = \dfrac{h(2x+h)}{h} = 2x+h \ .\)
Nu kan vi utan bekymmer låta \( h\to 0\) eftersom det inte påverkar något. Istället för att skriva \( \lim_{h\to 0}\) före varje kvot, vilket kan vara ganska jobbigt, så kan man förenkla differenskvoten som vi gjort hittils och sedan skriva
\( 2x+h \to 2x = f'(x), \ \mathrm{d}\unicode{0x00E5} \ h \to 0\)
Detta visar att derivatan av \( f(x) = x^2+1\) är \( f'(x) = 2x\)
Svar: \( f'(x) = 2x\).
b. Vi börjar med att beräkna \( f(x+h)\) som sist, så vi kan sätta upp differenskvoten.
\( f(x) = 4x+3 \\ f(x+h) = 4(x+h)+3\)
som alltså ger differenskvoten
\( \dfrac{f(x+h)-f(x)}{h} = \dfrac{(4(x+h)+3)-(4x+3)}{h} = \dfrac{4x+4h+3-4x-3}{h} = \dfrac{4h}{h} = 4 \ .\)
Här behöver vi inte ens låta \( h\) gå mot 0 eftersom vi inte har något \( h\) kvar! Om vi tar en sekund och kollar på vad vi nyss har beräknat. Vi hade en linjär funktion med k-värdet 4, som är lutningen och alltså derivatan! Vi fick även ut att \( f'(x) = 4\) ur derivatans definition, så matematiken ser ut att stämma.
Svar: \( f'(x) = 4\)
Övning
\( f'(x) = \lim_{h\to 0} \dfrac{f(x+h)-f(x)}{h} = \lim_{h\to 0} \dfrac{(x+h)^2+5-x^2-5}{h} = \\ = \lim_{h\to 0} \dfrac{x^2+2xh+h^2+5-x^2-5}{h} = \lim_{h\to 0} \dfrac{h(2x+h)}{h} =\\=\lim_{h\to 0} 2x+h = 2x\)
som ger \( f'(3) = 2 \cdot 3 = 6 \ .\)